Question

1. Suppose you have just received a shipment of 100 iPads where 7 iPads are defective. To determine whether or not you will accept the shipment, you randomly select 3 iPads and test them. If all 3 of the tablets works, you accept the shipment, if not, you reject it. What is the probability of rejecting the shipment

Answer 1

`p(x\geq 1)=0.1975`

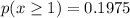
Explanation:

the probability that x iPads are defective in the sample follows a hypergeometric distribution, so it is calculated as:

`p(x)=(kCx*((N-k)C(n-x)))/(NCn)`

Where
`aCb=(a!)/(b!(a-b)!)`

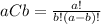
Because we have a N elements with k elements that are defective and we are going to take a sample of n elements. So, replacing N by 100, k by 7 and n by 3, we get:

`p(x)=(7Cx*((100-7)C(3-x)))/(100C3)`

Now, the probability of rejecting the shipment is the probability that at least one iPad of the sample is defective, so:

`p(x\geq 1)=p(1)+p(2)+p(3)`

Then:

`p(1)=(7C1*((100-7)C(3-1)))/(100C3)=0.1852\\p(2)=(7C2*((100-7)C(3-2)))/(100C3)=0.0121\\p(3)=(7C3*((100-7)C(3-3)))/(100C3)=0.0002`

Finally, the probability of rejecting the shipment is:

`p(x\geq 1)=0.1852+0.0121+0.0002=0.1975`