Answer:
a) 2.037 ohm/meter
b) 1487.9 Ω
Step-by-step explanation:
a)
We all know that:
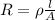
where:
 = resistivity
= resistivity
and which can be written as:
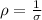
where
 = conductivity
= conductivity
l = length = 2 cm =
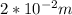
A = area =
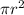
where
r = radius of the cylinder
r =
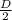
=
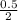
= 0.25 cm
Also by ohm's law
V = I R

=
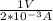
= 500 Ω
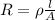
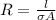
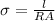
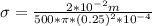
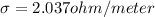
b)
Since
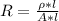
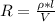
where ; V =

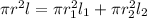
r = 0.25 cm, l = 2cm ,
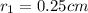 ,
,

So ; we are tasked to determine
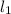 and
and
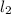
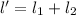


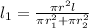

= 1.724 cm
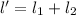
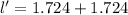
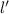 ≅ 3.45 cm
≅ 3.45 cm
Total Resistance R' is calculated as follows:
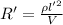
=
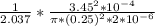
R' = 1487.9 Ω