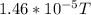Question

One long wire lies along an x axis and carries a current of 43 A in the positive x direction. A second long wire is perpendicular to the xy plane, passes through the point (0, 5.1 m, 0), and carries a current of 72 A in the positive z direction. What is the magnitude of the resulting magnetic field at the point (0, 0.60 m, 0)

Answer 1

`1.46*10^(-5)T`

Step-by-step explanation:

Using the magnetic field equation:

`B = \frac {\mu_oI} {2p r}`

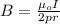
where:

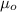`\mu_o` = permeability of free space =
`4p*10^(-7)T*m/A`

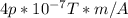
I = current in the wire

r = distance from the wire to the point

Magnetic field due to the wire on the x- axis can be calculated as:

`B = \frac {\mu_oI} {2p r}`

`B= (4p*10^(-7)*43)/(2p*0.60)`

`B = 1.43 *10^(-5) T`

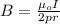
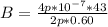
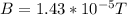
Magnetic field due to the positive z-direction wire:

`B = (\mu_ol)/(2pr)`

`B = (4p*10^(-7)*72)/(2p*5.1)`

`B = 2.82 *10^(-6)T`

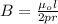
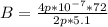
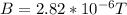
Now; adding these two vector components together to get the magnitude of the resultant vector; we have:

=
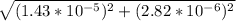
`\sqrt{(1.43 *10^(-5))^2+(2.82 *10^(-6))^2}`

=
`1.46*10^(-5)T`