Answer:
t-distribution should be used to test a claim : μ > $3000.
Explanation:
We are given that a random sample of 10 college students has a mean earnings of $3,120 with a sample standard deviation of $677 over the summer months.
We have to test a claim of μ > $3,000.
Since in this question we are provided with;
Sample mean earnings,
 = $3,120
= $3,120
Sample standard deviation, s = $677
Sample of college students, n = 10
So, Null Hypothesis,
 :
:
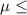 $3,000
$3,000
Alternate Hypothesis,
 :
:
 > $3,000
> $3,000
The distribution that we will use here for our test statistics will be t-distribution because in the question we don't know anything about population standard deviation
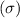 .
.
Normal distribution is used when we know population standard deviation
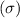 .
.
So, the test statistics used will be One-sample t-test statistics;
Test statistics =
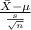 ~
~

Therefore, t-distribution should be used to test a claim: μ > $3000.