Answer:
Probability that the sample mean will be between $402.6 and $410.4 is 0.2689.
Explanation:
We are given that a bank has kept records of the checking balances of its customers and determined that the average daily balance of its customers is $413 with a standard deviation of $68.
A random sample of 61 checking accounts is selected.
Let
 = sample mean
= sample mean
Now, the z score probability distribution for sample mean is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = average daily balance of its customers = $413
= average daily balance of its customers = $413
 = standard deviation = $68
= standard deviation = $68
n = sample of checking accounts = 61
So, probability that the sample mean will be between $402.6 and $410.4 is given by = P($402.6 <
 < $410.4) = P(
< $410.4) = P(
 < $410.4) - P(
< $410.4) - P(

 402.6)
402.6)
P(
 < $410.4) = P(
< $410.4) = P(
 <
<
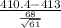 ) = P(Z < -0.29) = 1 - P(Z
) = P(Z < -0.29) = 1 - P(Z
 0.29)
0.29)
= 1 - 0.61409 = 0.38591
P(

 $402.6) = P(
$402.6) = P(


 ) = P(Z
) = P(Z
 -1.19) = 1 - P(Z < 1.19)
-1.19) = 1 - P(Z < 1.19)
= 1 - 0.88298 = 0.11702
Therefore, P($402.6 <
 < $410.4) = 0.38591 - 0.11702 = 0.2689
< $410.4) = 0.38591 - 0.11702 = 0.2689
Hence, probability that the sample mean will be between $402.6 and $410.4 is 0.2689.