Question

A company is bidding on two projects, A and B. The probability that the company wins project A is 0.40 and the probability that the company wins project B is 0.25. Winning project A and winning project B are independent events. What is the probability that the company wins project A or project B

Answer 1

The probability that the company wins either project A or B is 0.55 or 55%, calculated using the addition rule for independent events.

Step-by-step explanation:

The student asked about the probability of a company winning either project A or project B, given that the two events are independent. To find the probability that the company wins either project A or B (P(A OR B)), we use the addition rule of probability for independent events:

P(A OR B) = P(A) + P(B) − P(A AND B)

We are given that P(A) = 0.40 and P(B) = 0.25. Since A and B are independent, the probability of A and B happening together (P(A AND B)) is the product of their individual probabilities:

P(A AND B) = P(A) × P(B) = 0.40 × 0.25 = 0.10

Now we can calculate P(A OR B):

P(A OR B) = 0.40 + 0.25 − 0.10 = 0.55

Therefore, the probability that the company wins either project A or project B is 0.55 or 55%.

Answer 2

Probability that the company wins project A or project B is 0.50.

Step-by-step explanation:

We are given that a company is bidding on two projects, A and B. The probability that the company wins project A is 0.40 and the probability that the company wins project B is 0.25.

Also, Winning project A and winning project B are independent events.

Let the Probability of winning project A = P(A) = 0.40

Probability of winning project B = P(B) = 0.25

Now, as we know that ;

Probability that the company wins project A or project B =
`P(A \bigcup B)`

`P(A \bigcup B) = P(A) + P(B) - P(A \bigcap B)`

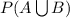
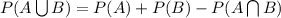
So, we have to find the value of Probability of winning project A and B, i.e;

`P(A \bigcap B)`

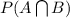
Since, we are given that Winning project A and winning project B are independent events which means when this condition is given then;

`P(A \bigcap B) = P(A) * P(B)`

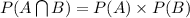
= 0.40
`*` 0.25 = 0.10

Now, Probability that the company wins project A or project B is given by;

`P(A \bigcup B) = P(A) + P(B) - P(A \bigcap B)`

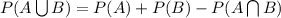
= 0.40 + 0.25 - 0.10

= 0.65 - 0.10 = 0.55

Hence, probability that the company wins project A or project B is 0.50.