Question

Suppose we purchase a larger bag of Skittles. Assume that this size bag always has 100 candies. In this particular bag 30 are green. 30 out of 100 is 30%. Is this a surprising result? Use the applet to conduct a simulation. Which option gives the right answer and the best explanation? Group of answer choices Yes, this is surprising. Random samples with this much error are unusual. Yes, this is surprising. We expect to see that 20% of candies are green. No, this is not surprising. This is about one and a half standard deviations above 20%. No, this is not surprising. We expect random samples to vary.

Answer 1

Yes, this is surprising. Random samples with this much error are unusual.

Explanation:

The expected proportion of green candies in the bag is p=0.20.

We have a sample with proportion p=0.3.

The amount of candies in the bag are 100.

We can calculate the probabilities of having 30 candies out of a sample of size n=100, if the proportion of the population is p=0.2.

This can be modeled by a binomial distribution with these parameters:

`\mu=np=100*0.2=20\\\\\sigma=√(npq)=√(100*0.2*0.8)=√(16)=4`

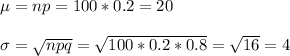
Then, the probability of having 30 or more candy in the bag is (applying the continuity factor):

`z=(X-\mu)/\sigma=(29.5-20)/4=9.5/4=2.375\\\\\\P(X>30)=P(z>2.375)=0.00877\approx 0.01`

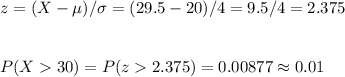
There is too little probability (1%) of having 30 green candies in the bag.