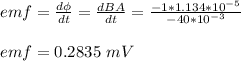Question

A magnetic field is uniform over a flat, horizontal circular region with a radius of 1.90 mm, and the field varies with time. Initially the field is zero and then changes to 1.50 T, pointing upward when viewed from above, perpendicular to the circular plane, in a time of 105 ms.

a. what is the average induced emf around the border of the circular region?
b. Immediately after this, in the next 65.0 ms, the magnetic field changes to a magnitude of 0.500 T, pointing downward when viewed from above. What is the average induced emf around the border of the circular region over this time period?

Answer 1

(a) The induced emf is 0.162 mV

(b) The induced emf is 0.2835 mV

Step-by-step explanation:

Given;

radius of the circular region, r = 1.90 mm = 1.9 x 10⁻³ m

`emf = (d \phi)/(dt)`

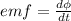
ΔΦ = ΔBA

where;

ΔΦ is change in magnetic flux

ΔB is the change in the strength of magnetic field

A is the area of the circular region

Area of the circular region:

A = πr² = π (1.9 x 10⁻³)² = 1.134 x 10⁻⁵ m²

Part (a) the average induced emf around the border of the circular region

`emf = (d \phi)/(dt) = (BA)/(t) = (1.5*1.134*10^(-5))/(105*10^(-3)) \\\\emf = 0.162 \ mV`

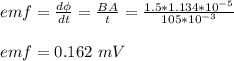
Part (b) the average induced emf around the border of the circular region

initial magnetic field strength, B₁ = 1.50 T

final magnetic field strength, B₂ = 0.500 T

Change in magnetic strength, ΔB = 0.5 - 1.5 = - 1 T

initial time period, t₁ = 105 ms

final time period, t₂ = 65 ms

Change in time period, Δt = 65 - 105 = - 40 ms

`emf = (d \phi)/(dt) = (dBA)/(dt) = (-1*1.134*10^(-5))/(-40*10^(-3)) \\\\emf = 0.2835 \ mV`