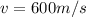Question

If the third charge (–| q 3 |) is placed at point P, but not held fixed, it will experience a force and accelerate away from the other two charges. If q3 = q = –1.0 nC, the mass of the third charge m3 is 5.0 x 10-12 kg, and s = 4.0 cm, what will the speed of charged particle #3 [in m/s] be after it has moved a very large distance away?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

A

The potential of this system is
`U=6.75*10^(-7)J`

B

The electric potential at point p is
`V_p= -900V`

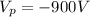
C

The work required is
`W= 9*10^(-7)J`

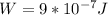
D

The speed of the charge is
`v=600m/s`

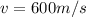
Step-by-step explanation:

A sketch to explain the question is shown on the second uploaded image

Generally the potential energy for a system of two charges is mathematically represented as

`U = (kq_1 q_2)/(d)`

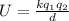
where k is the electrostatic constant with a value of
`k = 9*10^9 N m^2 /C^2`

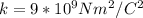
q is the charge with a value of
`q = 1*10^(-9)C`

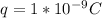
d is the distance given as
`d =5m`

Now we are given that
`q_1 = q` and
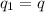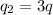`q_2 = 3q` and

Now substituting values

`U = (9*10^9 *1*10^(-9) * 3*10^(-9))/(5)`

`U=6.75*10^(-7)J`

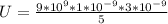
The electric potential at point P is mathematically obtained with the formula

`V_p = V_(-q) + V_(-3q)`

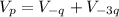
I.e the potential at
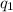`q_1` plus the potential at
`q_2`

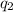
Now potential at
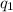`q_1` is mathematically represented as

`V_(-q) = (-kq)/(s)`

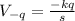
and the potential at
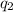`q_2` is mathematically represented as

`V_(-3q) = (-3kq)/(s)`

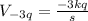
Now substituting into formula for potential at P

`V_p = (-kq)/(s) + (-3kq)/(s) = -(4kq)/(s)`

`= (4*9*10^9 *1*10^(-9))/(4*10^(-2))`

`V_p= -900V`

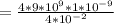
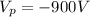
The Workdone to bring the third negative charge is mathematically evaluated as

`W =\Delta U = (kq_1q_3)/(s) + (kq_2q_3)/(s)`

`= (kq*q)/(s) + (kq*3q)/(s)`

`= (4kq^2)/(s)`

`= (4* 9*10^9 * (1*10^(-9))^2)/(4*10^(-2))`

`W= 9*10^(-7)J`

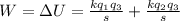
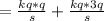
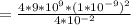
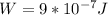
From the Question are told that the charge
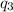`q_3` would a force and an acceleration which implies that all its potential energy would be converted to kinetic energy.This can be mathematically represented as

`\Delta U = W = (1)/(2) m_(q_3) v^2`

`9*10^(-7) = (1)/(2) m_(q_3) v^2`

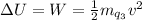
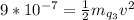
Where
`m_(q_3) = 5.0*10^(-12)kg`

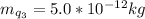
Now making v the subject we have

`v = \sqrt{(9*10^(-12))/(5*10^(-12)*0.5) }`

`v=600m/s`