Question

The mean number of children among a sample of 15 low-income households is 2.8. The mean number of children among a sample of 19 high-income households is 2.4. The standard deviations for low- and high-income households are found to be 1.6 and 1.7, respectively. Test the hypothesis of no difference against the alternative that high-income households have fewer children. Use a = 0.05 and a pooled estimate of the variance.

Answer 1

Explanation:

Let's put the data as below:

n1=15 x1=2.8 s1=1.6 and s1²=2.56

n2=19 x2=2.4 s2=1.7 and s2²=2.89

alpha= 0.05

To test the hypothesis:

H0= There is no sufficient evidence that low income household have fewer children

H1=There is sufficient evidence that low income household have fewer children

Assume that population variances are equal.

the t-static for two samples,

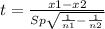`t=\frac{x1-x2}{Sp\sqrt{(1)/(n1)-(1)/(n2) \\} } }` ~t with min (n1-1,n2-1)df

The pooled variance estimate Sp equals:

`Sp^(2)=((n1-1)s1^(2)+(n2-1)s2^(2) )/(n1+n2-2)`

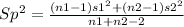
Sp²=2.7456

Sp=1.65699

Degrees of freedom=n1+n2-2=32

Under null hypothesis:

`tcal=\frac{1.6599\sqrt{(1)/(15)+(1)/(19) } }`

`tcal=0.6989`

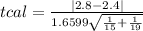
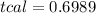
The critical value ttab=2.0369 for alpha=0.05

So we reject our null hypothesis H0

So there is sufficient evidence that low income households have fewer children than high income households