Question

A random sample of 16 values is drawn from a mound-shaped and symmetric distribution. The sample mean is 11 and the sample standard deviation is 2. Use a level of significance of 0.05 to conduct a two-tailed test of the claim that the population mean is 10.5.

Answer 1

We conclude that the population mean is different from 10.5.

Explanation:

We are given that a random sample of 16 values is drawn from a mound-shaped and symmetric distribution. The sample mean is 11 and the sample standard deviation is 2.

We have to test the claim that the population mean is 10.5.

Let, NULL HYPOTHESIS,
`H_0` :
`\mu` = 10.5 {means that the population mean is 10.5}

ALTERNATE HYPOTHESIS,
`H_a` :
`\mu \\eq` 10.5 {means that the population mean is different from 10.5}

The test statistics that will be used here is One-sample t-test;

T.S. =
`(\bar X - \mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

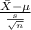where,
`\bar X` = sample mean = 11

s = sample standard deviation = 2

`\mu` = population mean

n = sample of values = 16

So, test statistics =
`(11-10.5)/((2)/(√(16) ) )` ~
`t_1_5`

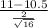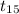
= 1

Now, at 0.05 significance level, t table gives a critical value of 2.131 at 15 degree of freedom. Since our test statistics is way less than the critical value of t so we have insufficient evidence to reject null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the population mean is different from 10.5.