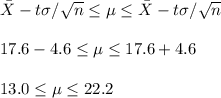Question

Refer to the accompanying data display that results from a sample of airport data speeds in Mbps. Complete parts​ (a) through​ (c) below. TInterval ​(13.046,22.15) x overbarequals17.598 Sxequals16.01712719 nequals50 a. Express the confidence interval in the format that uses the​ "less than" symbol. Given that the original listed data use one decimal​ place, round the confidence interval limits accordingly. nothing Mbpsless thanmuless than nothing Mbps ​(Round to two decimal places as​ needed.) b. Identify the best point estimate of mu and the margin of error. The point estimate of mu is nothing Mbps. ​(Round to two decimal places as​ needed.) The margin of error is Eequals nothing Mbps. ​(Round to two decimal places as​ needed.) c. In constructing the confidence interval estimate of mu​, why is it not necessary to confirm that the sample data appear to be from a population with a normal​ distribution? A. Because the sample size of 50 is greater than​ 30, the distribution of sample means can be treated as a normal distribution. B. Because the sample standard deviation is​ known, the normal distribution can be used to construct the confidence interval. C. Because the population standard deviation is​ known, the normal distribution can be used to construct the confidence interval. D. Because the sample is a random​ sample, the distribution of sample means can be treated as a normal distribution.

Answer 1

Point estimation of the mean = 17.6

Error = 4.6

95% CI: 13.0 ≤ μ ≤ 22.2

The distribution can be approximated to a normal because the sample size n=50 is bigger than 30.

Explanation:

We have this information:

- Sample mean:

`\bar{X}=17.598`

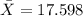
- Sample standard deviation

`s=16.01712719`

- Sample size

`n=50`

For now on, we round to one decimal place.

The best estimation for the population mean is the sample mean

`\mu=\bar{X}=17.6`

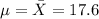
The margin of error is equal to the t-value multiplied by the sample standard deviation and divided by the sample size.

The t value depends on the degrees of freedom and the width of the confidence interval. In this case it is a 95% CI and the degrees of freedom are 49. For this conditions, the t-value is t=2.01.

Then, the margin of error is

`E=t_(49)*\sigma/√(n)=2.01*16.0/√(50)=4.553`

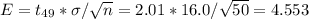
Then, the confidence interval can be constructed as:

`\bar{X}-t\sigma/√(n)\leq\mu\leq\bar{X}-t\sigma/√(n)\\\\17.6-4.6\leq \mu \leq 17.6+4.6\\\\ 13.0\leq \mu \leq 22.2`