Answer:
Therefore, the length of the square is
 cm which should be cut out of each corner to get a box with the maximum volume.
cm which should be cut out of each corner to get a box with the maximum volume.
Explanation:
Given that, an open box is made from a plastic with dimension 70 cm by 96 cm by removing a square from each corner of the plastic.
Consider, x be the length of the side of the square.
After cutting the corner, the length of the plastic is = (70-2x) cm
The width of the plastic is=(96-2x) cm.
Now the length of the open box = (70-2x) cm
The width of the open box = (96-2x) cm.
Then x will be the height of the open box.
The volume of the box is
V=Length×width×height
=[(70-2x) (96-2x) x] cm³
=(6720x -192x²-140x²+4x³) cm³
=(4x³-332x²+6720x) cm³
∴V=4x³-332x²+6720x
Differentiating with respect to x
V'= 12x²-664x+6720
Again differentiating with respect to x
V''= 24x -664
To find maximum volume, we set V' =0
12x²-664x+6720=0
⇒4(3x²-166x+1680)=0
⇒3x²-166x+1680=0
⇒3x²-126x-40x+1680=0
⇒3x(x-42)-40(x-42)=0
⇒(x-42)(3x-40)=0

Now
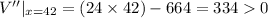
And
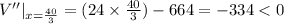 At
At
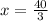 , V has maximum value.
, V has maximum value.
Therefore, the length of the square is
 cm which should be cut out of each corner to get a box with the maximum volume.
cm which should be cut out of each corner to get a box with the maximum volume.