first off let's change the mixed fractions to improper fractions, and let's Hailey's account first.
![\stackrel{mixed}{9(1)/(4)}\implies \cfrac{9\cdot 4+1}{4}\implies \stackrel{improper}{\cfrac{37}{4}} ~\hfill \stackrel{mixed}{8(7)/(8)}\implies \cfrac{8\cdot 8+7}{8}\implies \stackrel{improper}{\cfrac{71}{8}} \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/jsyqcgixby3bf19ev4j8.png)

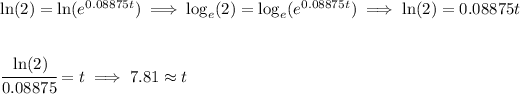
ok, now we know how long it takes for Hailey's money to double, how much money does Aiden have by then?

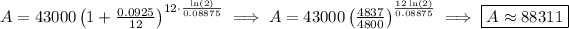
notice, in Hailey's amount we used the logarithmic value for "t", just to avoid any rounding issues.