Answer:
-∞ < x < -5 ∪ -5 < x < -3/2 ∪ -3/2 < x < ∞
Explanation:
The domain of any polynomial is "all real numbers." The domain of any rational function excludes any values of the variable that result in the denominator being 0. The function is "undefined" there.
__
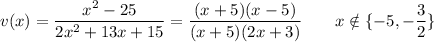
The values x=-5 and x=-3/2 make the denominator of v(x) become 0, so those values are excluded from the domain of v(x). The function is "undefined" when its denominator is zero.
-∞ < x < -5 ∪ -5 < x < -3/2 ∪ -3/2 < x < ∞
_____
Additional comment
The numerator and denominator factors (x+5) cancel each other, so there is no vertical asymptote at x=-5. Rather, the function has a "hole" there, where it is undefined. The limit as the function approaches x=-5 from either direction is v(x) = 10/7.