Question

A housing official in a certain city claims that the mean monthly rent for apartments in the city is more than $1000. To verify this claim, a simple random sample of 40 renters in the city was taken, and the sample mean rent paid was $1100 with a sample standard deviation of $300. Can you conclude that the mean monthly rent in the city is greater than $1000

Answer 1

Yes, we can conclude that the mean monthly rent in the city is greater than $1000.

Explanation:

We are given that a housing official in a certain city claims that the mean monthly rent for apartments in the city is more than $1000.

To verify this claim, a simple random sample of 40 renters in the city was taken, and the sample mean rent paid was $1100 with a sample standard deviation of $300.

Let, Null Hypothesis,
`H_0` :
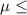`\mu \leq` $1000 {means that the mean monthly rent for apartments in the city is less than or equal to $1000}

Alternate Hypothesis,
`H_a` :
`\mu` > $1000 {means that the mean monthly rent for apartments in the city is more than $1000}

The test statistics that will be used here is t-test statistics;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean rent paid = $1100

s = sample standard deviation = $300

n = sample of renters = 40

So, test statistics =
`(1100-1000)/((300)/(√(40) ) )` ~
`t_3_9`

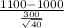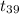
= 2.1082

Since in the question we are not given the significance level to test this hypothesis, so we assume it to be 5%. At 5% level of significance, t table gives critical value of 1.685 at 39 degree of freedom. Since our test statistics is more the critical value of t so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the mean monthly rent in the city is greater than $1000.