Answer:
Therefore the mass of the of the oil is 409.59 kg.
Explanation:
Let us consider a circular disk. The inner radius of the disk be r and the outer diameter of the disk be (r+Δr).
The area of the disk
=The area of the outer circle - The area of the inner circle
=

![=\pi [r^2+2r\triangle r+(\triangle r)^2-r^2]](https://img.qammunity.org/2021/formulas/mathematics/college/4980wkl2qyhlms2sf4cbemvia1t1p1vyp7.png)
![=\pi [2r\triangle r+(\triangle r)^2]](https://img.qammunity.org/2021/formulas/mathematics/college/xdvcr3qko8ruzjogdfpllrx3a3uxrh5gtf.png)
Since (Δr)² is very small, So it is ignorable.
∴
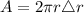
The density

We know,
Mass= Area× density
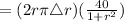
Total mass
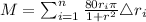
Therefore
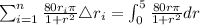
![=40\pi[ln(1+r^2)]_0^5](https://img.qammunity.org/2021/formulas/mathematics/college/askz90k0fsz04gmzochslt9lmxs6w8co3a.png)
![=40\pi [ln(1+5^2)-ln(1+0^2)]](https://img.qammunity.org/2021/formulas/mathematics/college/xkdvzkb15wjddom1kla08caasyi7f8ln97.png)

= 409.59 kg (approx)
Therefore the mass of the of the oil is 409.59 kg.