Answer : The pressure of the gas using both the ideal gas law and the van der Waals equation is, 60.2 atm and 44.6 atm respectively.
Explanation :
First we have to calculate the pressure of gas by using ideal gas equation.
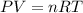
where,
P = Pressure of
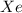 gas = ?
gas = ?
V = Volume of
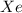 gas = 0.805 L
gas = 0.805 L
n = number of moles
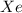 = 1.93 mole
= 1.93 mole
R = Gas constant =
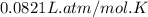
T = Temperature of
 gas = 306 K
gas = 306 K
Now put all the given values in above equation, we get:
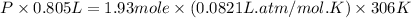
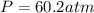
Now we have to calculate the pressure of gas by using van der Waals equation.
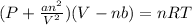
P = Pressure of
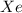 gas = ?
gas = ?
V = Volume of
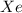 gas = 0.805 L
gas = 0.805 L
n = number of moles
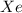 = 1.93 mole
= 1.93 mole
R = Gas constant =
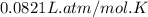
T = Temperature of
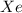 gas = 306 K
gas = 306 K
a = pressure constant =
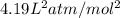
b = volume constant =
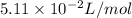
Now put all the given values in above equation, we get:
![(P+((4.19L^2atm/mol^2)* (1.93mole)^2)/((0.805L)^2))[0.805L-(1.93mole)* (5.11* 10^(-2)L/mol)]=1.93mole* (0.0821L.atm/mol.K)* 306K](https://img.qammunity.org/2021/formulas/chemistry/college/jy1oyri8cu6z1styigcbh9t5jvznqtken5.png)
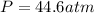
Therefore, the pressure of the gas using both the ideal gas law and the van der Waals equation is, 60.2 atm and 44.6 atm respectively.