Question

It's a snowy day and you're pulling a friend along a level road on a sled. You've both been taking physics, so she asks what you think the coefficient of friction between the sled and the snow is. You've been walking at a steady 1.5\;{\rm m}/{\rm s}, and the rope pulls up on the sled at a 42.0^\circ angle. You estimate that the mass of the sled, with your friend on it, is 73.0 kg and that you're pulling with a force of 87.0 N.?

Answer 1

0.0984

Step-by-step explanation:

From the first diagram attached below; a free flow diagram shows the interpretation of this question which will be used to solve this question.

From the diagram, the horizontal component of the force is:

`F_X = F_(cos \ \theta)`

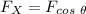
Replacing 42° for θ and 87.0° for
`F`

`F_X =87.0 \ N \ *cos \ 42 ^\circ`

`F_X =64.65 \ N`

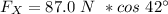
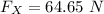
On the other hand, the vertical component is ;

`F_Y = Fsin \ \theta`

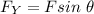
Replacing 42° for θ and 87.0° for
`F`

`F_Y =87.0 \ N \ *sin \ 42 ^\circ`

`F_Y =58.21 \ N`

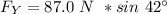
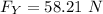
However, resolving the vector, let A be the be the component of the mutually perpendicular directions.

The magnitude of the two components is shown in the second attached diagram below and is now be written as A cos θ and A sin θ

The expression for the frictional force is expressed as follows:

`f = \mu \ N`

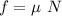
Where;

`\mu` is said to be the coefficient of the friction

N = the normal force

Similarly the normal reaction (N) = mg - F sin θ

Replacing
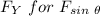`F_Y \ for \ F_(sin \ \theta)`. The normal reaction can now be:

`N = mg \ - \ F_Y`

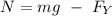
By balancing the forces, the horizontal component of the force equals to frictional force.

The horizontal component of the force is given as follows:

`F_X = \mu \ ( mg - \ F_Y)`

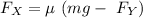
Making
`\mu` the subject of the formular in the above equation; we have the following:

`\mu \ = \ (F_X)/(mg - F_Y)`

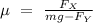
Replacing the following values: i.e

`F_X \ = \ 64.65 \ N`

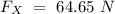
m = 73 Kh

g = 9.8 m/s²

`F_Y = \ 58.21 N`

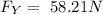
Then:

`\mu \ = \ (64.65 N)/((73.0 kg)(9.8m/s^2) - (58.21 \ N))`

`\mu = 0.0984`

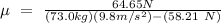
Thus, the coefficient of friction is = 0.0984