Explanation:
Let's represent the two integers with the variables
 and
and
 .
.
From the problem statement, we can create the following two equations:
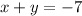
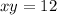
With the first equation, we can subtract
 from both sides to isolate the
from both sides to isolate the
 variable to the left-hand side:
variable to the left-hand side:
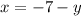
Now that we have a value for
 , we can plug it into the second equation and solve for
, we can plug it into the second equation and solve for
 :
:
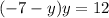
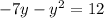
Now, let's move everything to one side of the equation:
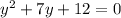
Factoring this quadratic will give us two values for
 :
:
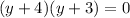
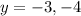
Since we now know
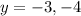 , we can plug this back into either of the original equations to get a value for
, we can plug this back into either of the original equations to get a value for
 , which will be
, which will be
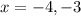 .
.
So the two numbers that sum to
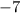 and have a product of
and have a product of
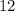 are
are
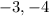 .
.