Question

Using a function on her calculator, Jamie can generate a single random digit by pressing the "Enter" key. She wants to experiment and see how many times it will take for her calculator to generate a fifth "4." Assume that the calculator will generate a "4" on any given attempt with probability 0.20. How many total generated digits should we expect in order to get a fifth "4"

Answer 1

We should expect 25 generated digits in order to get a fifth "4"

Explanation:

For each generated digit, there are only two possible outcomes. Either it is a four, or it is not. The probability of a digit being a 4 is independent of other digits. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

The expetcted number of trials to get r sucesses, with p probability, is given by:

`E = (r)/(p)`

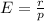
Assume that the calculator will generate a "4" on any given attempt with probability 0.20.

This means that
`p = 0.2`

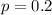
How many total generated digits should we expect in order to get a fifth "4"

This is E when r = 5. So

`E = (r)/(p) = (5)/(0.2) = 25`

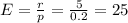
We should expect 25 generated digits in order to get a fifth "4"