Question

When heated, hydrogen sulfide gas decomposes according to the equation: 2H2S(g) → 2H2(g) + 2S2(g) A 6.75 gram sample of H2S(g) is introduced into an evacuated rigid 0.75 L container. The sealed container is heated to 283 K and 6.42 x 10 ^–2 mol of S2 gas is present at equilibrium.

a. Calculate the equilibrium concentration, in mol/L, of the H2(g) in the container at 283 K.
b. Calculate the equilibrium concentration, in mol/L, of the H2S(g) in the container at 283 K.
c. Calculate the value of the equilibrium constant, Kc, for the decomposition reaction at 283 K.
d. Calculate the partial pressure of S2(g) in atm in the container at equilibrium at 283 K.
e. Calculate the value of the equilibrium constant, Kc, for the reaction

H2(g) + 1/2 S2(g) → H2S (g) at 283 K.

Answer 1

a. 0.171M

b. 0.0938M

c. 0.284

d. 1.99atm

e. 1.88

Step-by-step explanation:

Hello,

In this case, for the given reaction whose balance should be corrected as:

`2H_2S(g) \rightleftharpoons 2H_2(g) + S_2(g)`

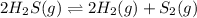
For which the law of mass action, in terms of the change
`x` due to stoichiometry and the reaction extent, turns out:

`K=([H_2]_(eq)^2[S_2]_(eq))/([H_2S]_(eq)^2)`

Thus, the initial concentration of hydrogen sulfide is:

`[H_2S]_0=(6.75g/(34g/mol))/(0.75L) =0.265M`

Now, since the equilibrium amount of sulfur is given, the change
`x` due to equilibrium reaching is:

`[S_2]_(eq)=x=(6.42x10^(-2)mol)/(0.75L)=0.0856M`

Therefore:

a. Equilibrium concentration of hydrogen:

`[H_2]_(eq)=2x=2*0.0856M=0.171M`

b. Equilibrium concentration of hydrogen sulfide:

`[H_2S]_(eq)=0.265M-2x=0.265M-2*0.0856M=0.0938M`

c.) Equilibrium constant, Kc:

`Kc=((0.171)^2(0.0856))/((0.0938)^2)=0.284`

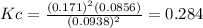
d.) Partial pressure of sulfur gas:

`p_(S_2)=[S_2]RT= 0.0856(mol)/(L)*0.082(atm*L)/(mol*K)*283K=1.99atm`

e. Kc, for the reaction:

`H_2(g) + (1)/(2) S_2(g)\rightleftharpoons H_2S(g)`

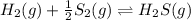
In that case, it equals the inverse halved initial reaction, whose modification is related as:

`Kc_2=(1)/(√(Kc) ) =(1)/(√(0.284) ) =1.88`

Best regards.