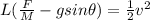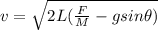Question

As in Problem A above, a block of mass M starts from rest and is pushed up a frictionless ramp inclined at an angle θ above the horizontal by a constant force F. Use the work-energy theorem to find the block’s speed after it has been pushed a distance L up the incline. Your answer should be written in terms of M, θ, F, L and the acceleration due to gravity, g.

Answer 1

A(i)

The solution to this question is shown on the second uploaded image

A(ii)

The final speed is
`v = \sqrt{2L ((F)/(M) - gsin\theta )}`

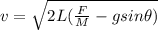
B

The block speed after a distance L is
`v= \sqrt{2L ((F)/(M) -gsin \theta )}`

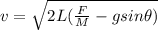
Step-by-step explanation:

From the question

The net force i the x-direction is mathematically represented as

`F_(net) = Ma`

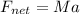
From the the diagram in the second uploaded image we see that

`F_(net) = F - Mgsin \theta`

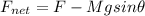
Therefore

`F- Mgsin\theta = Ma`

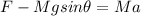
Making a the subject

`a = (F)/(M) - gsin\theta`

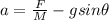
Applying the law of motion

`v^2 =u^2 + 2as`

where u = 0 m/s and s =L

`v^2 = 0 + 2((F)/(M) - gsin \theta )L`

=>
`v = \sqrt{2L ((F)/(M) - gsin\theta )}`

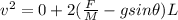
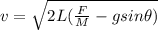
According to Energy conservation law and work theorem

Workdone by F + Workdone by gravity = change in kinetic energy

Mathematically this is given as

`F * L - (mgsin \theta)L = (1)/(2) M (v^2-u^2)`

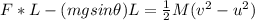
Since u = 0 m/s

`L ((F)/(M) - gsin \theta ) = (1)/(2) v^2`

`v= \sqrt{2L ((F)/(M) -gsin \theta )}`