Answer:
The proportion of women that have blood pressures lower than 64 is P(x<64) = P(z<-1.68) = 0.04648 or about 0.05 (5% of the cases) or 4.6/100 (about 5/100); that is, approximately, five of one hundred women have blood pressures lower than 64 (rounding to the nearest integer).
Explanation:
To solve this, we need to use the cumulative standard normal distribution and use the z-score of the raw value x = 64 to find the proportion of women having blood pressures lower than 64.
The z-score is a "transformation" of the raw score to use the cumulative standard normal distribution. We can obtain this using the following formula:

Where
 is the population mean. In this case,
is the population mean. In this case,
 .
.
 is the population standard deviation. In this case,
is the population standard deviation. In this case,
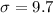
The x is the raw value. In this case, x = 64.
The proportion of women that have blood pressures lower than 64
The z-score is
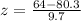
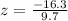
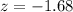
This value for z tells us that is -1.68 is standard deviations below the mean (notice the negative sign).
The normal distribution (and also the standard normal distribution) are symmetrical. Because of this, the cumulative probability P(z<-1.68) is the same that 1 - P(z<1.68) = P(z>1.68).
In this way, consulting a standard cumulative normal table (available on Internet or textbooks in Statistics), the cumulative probability for P(z<1.68) = 0.95352. Then
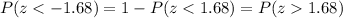
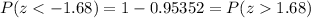

Thus, the proportion of women that have blood pressures lower than 64 is P(x<64) = P(z<-1.68) = 0.04648 or about 0.05 (5% of the cases). That is, 4.6/100 or 5/100 (rounding to the nearest integer) or nearly five of one hundred women have this condition.
The graph below shows the shaded area that corresponds to the proportion of 0.04648 (or about 0.05), for a normal distribution of mean = 80.3 and a standard deviation = 9.7.