Question

Vehicles leave an airport parking facility (arrive at parking fee collection booths) at a rate of 500 veh/h (the time between arrivals is exponentially distributed). The parking facility has a policy that the average time a patron spends in a queue waiting to pay for parking is not to exceed 5 seconds. If the time required to pay for parking is exponentially distributed with a mean of 15 seconds, what is the smallest number of payment processing booths that must be open to keep the average time spent in a queue below 5 seconds?

Answer 1

At least 3 processing booths should be open.

Explanation:

1 vehicle spends an average of 15 seconds in a booth

In N booths , there will be N/15 vehicles in 1 second

In 1 hr, there will be N/15 * 3600 vehicles

Therefore, there will be a total of 240N vehicles/hour

Actual arrival rate of vehicles at the airport is 500 veh/h

Probability of arrival, P =
`(Number of possible outcomes)/(Total outcomes)`

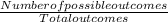
P = 500/240N

P = 2.083/N

For the average time spends to be below 5 seconds

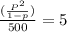`(((P^(2) )/(1-p) ))/(500) = 5`, since 500 is the average value.

`(P^(2) )/(1-p) } = 2500\\P^(2) = 2500 (1-P)\\P^(2) = 2500 - 2500P\\((2.083)/(N)) ^(2) = 2500 - 2500((2.083)/(N))`

`2.083^(2) = 2500N^(2) - 5208N\\2500N^(2) - 5208N - 4.34 = 0`

`N^(2) -2.0832N - 0.0017 = 0`

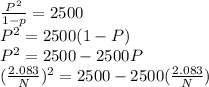
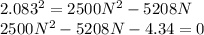
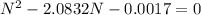
Solving for N using the quadratic formula with a = 1, b = -2.0832, c = -0.0017

`N = \frac{-b \pm \sqrt{b^(2) -4ac} }{2a} \\N = \frac{2.0832 \pm \sqrt{(-2.0832)^(2) -4*1*(-0.0017)} }{2}`

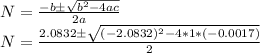
N = 1.0416 ± 1.0424

N = 2.084 or -0.0008

N = 2.084 is the only realistic value here

Therefore, the smallest number of processing booths that must be open should be 3