Question

A potter’s wheel—a thick stone disk of radius0.500 mand mass 100 kg—is freely rotating at 50.0 rev/min.The potter can stop the wheel in 6.00 s by pressing awet rag against the rim and exerting a radially inwardforce of 70.0 N. Find the effective coefficient of kineticfriction between wheel and rag.

Answer 1

- 0.873rad/
`s^(2)`

angular velocity = -0

Step-by-step explanation:

Given the mass of the disk is 100kg

the radius of the disk is 0.500m

the normal force on the disk is 700N

the normal force that acts radial inward is 70.0N

the final rotation of the wheel is 0.500rev/s and the initial rotation of wheel is 0

Formula to calculate the mass moment of inertia is

`I = (1)/(2) MR^(2)`

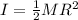
where I is the mass of inertia

R is the radius of the disk

M is the mass of the disk

substitute 100kg for M and 0.500m for R in above equation to find I

I = 1/2(100kg)(0.500m)∧2

I = 12.5kg.m∧2

thus the mass moment of inertia is 12.5kg.m∧2

formula to calculate the angular acceleration is

∝ = ωf - ωi/ t

here ∝ = angular acceleration

ωf = final angular speed

ωi = initial angular speed

t = the time taken to stop the wheel by potter.

t = 2.00s

ωf = 0.500rev/s

ωi = 0

in the equation above to find ∝

∝
`= (0-5.24rev/s((x)/(180) )((360)/(60s) ))/(2.00s)`

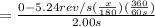
∝ = -0.873rad/
`s^(2)`

thus the angular acceleration is -0