Question

Coherent light with wavelength 540 nm passes through narrow slits with a separation of 0.370 mm .Part AAt a distance from the slits which is large compared to their separation, what is the phase difference (in radians) in the light from the two slits at an angle of 25.0 ∘ from the centerline?

Answer 1

The phase difference between waves 31.7 rad

Step-by-step explanation:

Given :

Wavelength
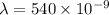`\lambda = 540 * 10^(-9)` m

Separation between two slit
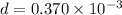`d = 0.370 * 10^(-3)` m

Angle
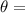`\theta =` 25°

From the formula of phase difference,

`\delta = (2\pi d )/(\lambda) \sin \theta`

Where
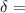`\delta =` phase difference

`\delta = (2 * \pi * 0.370 * 10^(-3) )/(540 * 10^(-9) ) \sin 25`

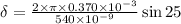
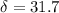`\delta = 31.7` rad

Therefore, the phase difference between waves 31.7 rad