Question

A 0.629 g sample of a diprotic acid is dissolved in water and titrated with 0.270 M NaOH. What is the molar mass of the acid if 36.4 mL of the NaOH solution is required to neutralize the sample? Assume the volume of NaOH corresponds to the second equivalence point. A flask with a solution sits on the base of a ring stand. A buret filled with liquid is suspended above the flask by the ring stand. molar mass: g/mol

Answer 1

Answer: The molar mass of acid is 127.97 g/mol

Step-by-step explanation:

To calculate the number of moles for given molarity, we use the equation:

`\text{Molarity of the solution}=\frac{\text{Moles of solute}* 1000}{\text{Volume of solution (in L)}}`

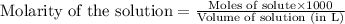
Molarity of NaOH solution = 0.270 M

Volume of solution = 36.4 mL

Putting values in above equation, we get:

`0.270M=\frac{\text{Moles of NaOH}* 1000}{36.4}\\\\\text{Moles of NaOH}=(0.270* 36.4)/(1000)=0.00983mol`

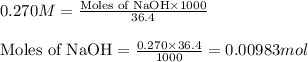
The chemical equation for the reaction of NaOH and diprotic acid follows:

`2NaOH+H_2X\rightarrow 2NaX+2H_2O`

By Stoichiometry of the reaction:

2 moles of NaOH reacts with 1 mole of diprotic acid

So, moles of diprotic acid =
`(0.00983)/(2)=0.004915moles`

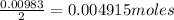
To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

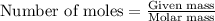
Mass of acid = 0.629 g

Moles of acid = 0.004915 moles

Putting values in above equation, we get:

`0.004915mol=\frac{0.629g}{\text{Molar mass of acid}}\\\\\text{Molar mass of acid}=(0.629g)/(0.004915mol)=127.97g/mol`

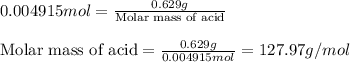
Hence, the molar mass of acid is 127.97 g/mol