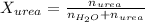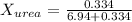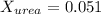Question

. You prepare a solution by adding 20.0 g Urea [(NH2)2CO] to 125 g water at 25.0oC & vapor pressure 23.76 torr. The solution vapor pressure is 22.67 torr. Calculate the molecular weight of urea. XH2O = ________ moles H2O = ________ Xsolute = ________ moles urea = ________ molar mass = ________ calculations:

Answer 1

Answer : The molecular wight of urea is, 59.9 g/mol

Mole fraction of water and urea is, 0.95 and 0.051 respectively.

Explanation :

According to the relative lowering of vapor pressure, the vapor pressure of a component at a given temperature is equal to the mole fraction of that component of the solution multiplied by the vapor pressure of that component in the pure state.

Formula used :

`(\Delta p)/(p^o)=X_b`

`(p^o-p_s)/(p^o)=(n_b)/(n_a+n_b)`

`(p^o-p_s)/(p^o)=((w_b)/(M_b))/((w_a)/(M_a)+(w_b)/(M_b))`

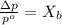
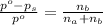
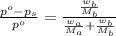
where,

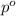`p^o` = vapor pressure of the pure solvent water = 23.76 torr

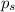`p_s` = vapor pressure of the solution = 22.67 torr

`X_b` = mole fraction of solute (urea)

n is the number of moles

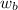`w_b` = mass of urea = 20.0 g

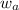`w_a` = mass of water = 125 g

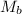`M_b` = molar mass of urea = ?

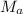`M_a` = molar mass of water = 18 g/mol

Now put all the given values in the above expression, we get:

`(23.76-22.67)/(23.76)=((20.0)/(M_b))/((125)/(18)+(20.0)/(M_b))`

`M_b=59.9g/mol`

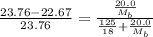
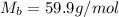
Now we have to calculate the moles of
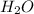`H_2O` and urea.

`\text{Moles of }H_2O=\frac{\text{Given mass }H_2O}{\text{Molar mass }H_2O}=(125g)/(18g/mol)=6.94mol`

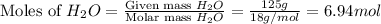
and,

`\text{Moles of urea}=\frac{\text{Given mass urea}}{\text{Molar mass urea}}=(20.0g)/(59.9g/mol)=0.334mol`

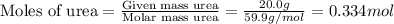
Now we have to calculate the mole fraction of
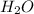`H_2O` and urea.

`X_(H_2O)=(n_(H_2O))/(n_(H_2O)+n_(urea))`

`X_(H_2O)=(6.94)/(6.94+0.334)`

`X_(H_2O)=0.95`

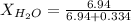
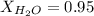
and,

`X_(urea)=(n_(urea))/(n_(H_2O)+n_(urea))`

`X_(urea)=(0.334)/(6.94+0.334)`

`X_(urea)=0.051`