Question

A cylindrical bucket is being filled with paint at a rate of 4 cm3 per minute. How fast is the level rising when the bucket starts to overflow? The bucket has a radius of 20 centimeters and a height of 70 centimeters. (Round your answer to four decimal places.)

Answer 1

Therefore,the level of paint is rising when the bucket starts to overflow at a rate
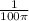`(1)/(100\pi)` cm per minute.

Explanation:

Given that, at a rate 4 cm³ per minute,a cylinder bucket is being filled with paint

It means the change of volume of paint in the cylinder is 4 cm³ per minutes.

i.e
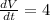`(dV)/(dt)= 4` cm³ per minutes.

The radius of the cylinder is 20 cm which is constant with respect to time.

But the level of paint is rising with respect to time.

Let the level of paint be h at a time t.

The volume of the paint at a time t is

`V=\pi r^2 h`

`\Rightarrow V=\pi (20)^2h`

`\Rightarrow V=400\pi h`

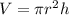
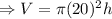
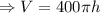
Differentiating with respect to t

`(dV)/(dt)=400\pi * (dh)/(dt)`

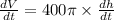
Now putting the value of
`(dV)/(dt)`

`\Rightarrow 4=400\pi (dh)/(dt)`

`\Rightarrow (dh)/(dt)=(4)/(400\pi)`

`\Rightarrow (dh)/(dt)=(1)/(100\pi)`

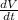
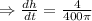
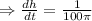
To find the rate of the level of paint is rising when the bucket starts to overflow i.e at the instant h= 70 cm.

`\left (dh)/(dt)\right|_(h=70)=(1)/(100\pi)`

Therefore, the level of paint is rising when the bucket starts to overflow at a rate
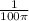`(1)/(100\pi)` cm per minute.