Question

From a survey of coworkers you find that 32​% of 150 have already received this​ year's flu vaccine. An approximate 98​% confidence interval is ​(0.231​, 0.409​). ​a) How would the confidence interval change if the sample size had been 600 instead of 150​? ​b) How would the confidence interval change if the confidence level had been 90​% instead of 98​%? ​c) How would the confidence interval change if the confidence level had been 99​% instead of 98​%?

Answer 1

a) Narrower

b) Narrower

c) Wider

Explanation:

We are given the following in the question:

Proportion of coworker who received flu vaccine = 32​%

98​% confidence interval: (0.231​, 0.409​)

Confidence interval:

`\hat{p}\pm z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

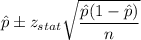
​a) Sample size had been 600 instead of 150​

If we increase the sample size, thus the standard error of the interval decreases.

Since the standard error decreases, the confidence interval become narrower.

b) Confidence level had been 90​% instead of 98​%

As the confidence level increases, the confidence interval becomes narrower. This is due to a smaller value of z-statistic at 90% confidence level.​

c) Confidence level had been 99​% instead of 98​%

As the confidence level increases, the width of the confidence interval increases and the confidence interval become wider. This is because of a larger value of z-statistic at 99% confidence interval.