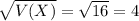Question

You are to take a multiple-choice exam consisting of 100 questions with 5 possible responses to each question. Suppose that you have not studied and so must guess (select one of the five answers in a completely random fashion) on each question. Let x represent the number of correct responses on the test. (a) What is your expected score on the exam? (Hint: Your expected score is the mean value of the x distribution.) (b) Compute the variance and standard deviation of x. Variance = Standard deviation =

Answer 1

a) 20

b) Variance 16, standard deviation 4

Explanation:

For each question, there are only two possible outcomes. Either you guesses the answer correctly, or you do not. The probability of guessing the answer of a question correctly is independent of other questions. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

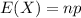
The variance of the binomial distribution is:

`V(X) = np(1-p)`

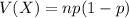
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

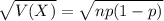
100 questions

So n = 100.

You guess

5 options, one correct. So
`p = (1)/(5) = 0.2`

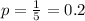
(a) What is your expected score on the exam?

`E(X) = np = 100*0.2 = 20`

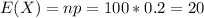
(b) Compute the variance and standard deviation of x.

Variance:

`V(X) = np(1-p) = 100*0.2*0.8 = 16`

Standard deviation:

`√(V(X)) = √(16) = 4`