Question

A quadratic equation is shown:

x2 - 14x + 41 = 0
Which of the following is the first correct step to write the above equation in the form (x - p)2 = 9, where p and q are integers?
x2 - 14x + 41 + 8 = 0 + 8
x2 - 14x + 41 + 9 = 0 + 9
x2 - 14x + 41 - 8 = 0 - 8
x2 – 14x + 41 - 9 = 0 - 9

Answer 1

The correct answer is the first option

Explanation:

Quadratic Equation

The standard form of a quadratic equation is

`ax^2+bx+c=0`

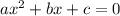
Sometimes we need to change the expression of the same equation to the form

`(x-p)^2=q`

To accomplish that change, we usually modify the left-hand expression to make it look like the square of a binomial.

The given quadratic equation is

`x^2-14x+41=0`

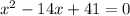
Recall the square of a binomial is

`(x-p)^2=x^2-2px+p^2`

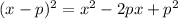
The first term is already present. The second term gives us the value of p:

`-2px=-14x`

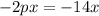
Solving

`p=7`

Now we need to produce the third term
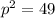`p^2=49`. We only have 41, thus we need to add 8 to both sides of the equation:

`x^2-14x+41+8=0+8`

The correct answer is the first option