Question

The area of a rectangular wall of a barn is 85 square feet. Its length is 12 feet longer than the width. Find the length and width of the wall of the barn.

Answer 1

Length = 17 feet, Width = 5 feet

Explanation:

Given:

The area of a rectangular wall of a barn is 85 square feet.

Its length is 12 feet longer than the width.

Question asked:

Find the length and width of the wall of the barn.

Solution:

Let width of a rectangular wall of a barn =
`x`

As length is 12 feet longer than the width.

Length of a rectangular wall of a barn =
`12+x`

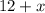
As we know:

`Area\ of\ rectangle=length* breadth`

`85=(12+x)x\\\\85=12x+x^(2) \\`

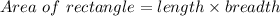
Subtracting both sides by 85

`x^(2) +12x-85=0\\x^(2) +17x-5x-85=0\\Taking\ common\\x+(x+17)-5x(x+17)=0\\(x+17)(x-5)=0\\x+17=0, x-5=0\\x=-17,x=5`

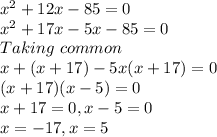
As width can never be in negative, hence width of a rectangular wall of a barn =
`x` = 5 feet

Length of a rectangular wall of a barn =
`12+x=12+5=17\ feet`

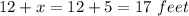
Therefore, length and width of the wall of the barn is 17 feet and 5 feet respectively.