Answer:
Both candles will have the same height after 4 hours.
Explanation:
The equation for the amount of candle remaining can be given by the following equations:
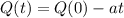
In which Q(t) is the amount after t hours, Q(0) is the initial amount and a is how much it decreases, in inches, per hour.
Red candle:
8 inches tall and burns at a rate of 7 divided by 10 inch per hour. This means that
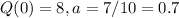 . So
. So
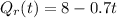
Blue candle:
6 inches tall and burns at a rate of 1 divided by 5 inch per hour. This means that
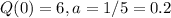 . So
. So

After how many hours will both candles be the same height ?
This is t when
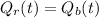
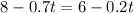
![0.2t - 0.7t = 6 - 8[/yrc]</p><p>[tex]-0.5t = -2](https://img.qammunity.org/2021/formulas/mathematics/high-school/g0nr8bz1x0rs0zx42zkfq641a1jbvtzql7.png)
Multiplying by (-1)
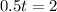
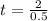
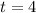
Both candles will have the same height after 4 hours.