Question

A play court on the school playground is shaped like a square joined by a semicircle the perimeter a round the entire play court is 182.8 feet and 62.8 feet of the total perimeter comes from the semicircle. After you get the answer explain how you got that?

Answer 1

Square side=40ft

Semi-circle diameter=39.98ft

Area of court=2276.69 ft^2

Explanation:

The square section has a semicircle joined to it and the combined perimeter is 182.8 ft.

-Area of the square section is obtained by subtracting that of the semicircle from the total(only 3 sides of the square is used since one side is attached to the semi-circle)

`A_T=A_(sc)+A_(sq)\\\\=(1)/(2)\pi D+3s\\\\=182.8=62.8+3s\\\\s=40\ ft`

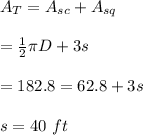
Hence, the square's sides has the dimension of 40 ft.

The semi-circle's diameter is calculated as:

`P=(1)/(2)\pi D\\\\62.8=0.5\pi D\\\\D=(62.8)/(0.5\pi)=39.98`

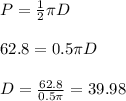
Hence, the semi-circle's diameter is 39.98 ft

The area of the court is calculated as:

`A=0.5\pi (D/2)^2+s^2\\\\=0.5*\pi * (39.98/2)^2+40^2\\\\=2227.69 \ ft^2`

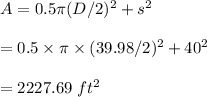
The court's area is 2,227.69 ft^2