Question

can company makes a cylindrical can that has a radius of 6 cm and a height of 10 cm. One of the company's clients needs a cylindrical can that has the same volume but is 15 cm tall. What must the new radius be to meet the client's need? Round to the nearest tenth of a centimeter.

Answer 1

Answer: Its 4.9 cm

Explanation:

Answer 2

the new radius be to meet the client's need is 4.9 cm .

Explanation:

Here we have , can company makes a cylindrical can that has a radius of 6 cm and a height of 10 cm. One of the company's clients needs a cylindrical can that has the same volume but is 15 cm tall. We need to find What must the new radius be to meet the client's need . Let's find out:

Let we have two cylinders of volume
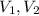`V_1 , V_2` with parameters as follows :

`r_1=6cm\\h_1=10cm\\r_2=?\\h_2=15cm`

We know that volume of cylinder is
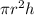`\pi r^2h` , According to question volume of both cylinder is equal i.e

⇒
`V_1=V_2`

⇒
`\pi (r_1)^2h_1= \pi (r_2)^2h_2`

⇒
`(r_1)^2h_1= (r_2)^2h_2`

⇒
`((r_1)^2h_1)/(h_2)= (r_2)^2`

⇒
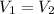
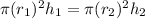
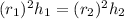
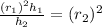
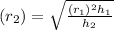`(r_2) =\sqrt{ ((r_1)^2h_1)/(h_2)}` Putting all values

⇒
`(r_2) =\sqrt{ ((6)^2(10))/(15)}`

⇒
`(r_2) =\sqrt{ (36(10))/(15)}`

⇒
`(r_2) =\sqrt{ (360)/(15)}`

⇒
`(r_2) =√(24)`

⇒
`(r_2) =4.9cm`

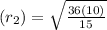
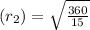
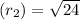
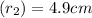
Therefore , the new radius be to meet the client's need is 4.9 cm .