Question

Help me understand this question

Answer 1

`x=2\ cm`

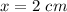
see the explanation

Explanation:

we know that

If two triangles are similar, then the ratio of its corresponding sides is proportional

In this problem

Triangle BAE and CAD are similar -----> given problem

so

using proportionality

`(BA)/(CA)=(AE)/(AD)`

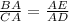
we have

`BA=10\ cm\\CA=(x+10)\ cm\\AE=15\ cm\\AD=15+3=18\ cm`

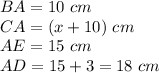
substitute the values

`(10)/(x+10)=(15)/(18)`

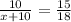
solve for x

`10(18)=15(x+10)\\180=15x+150\\15x=180-150\\15x=30\\x=2\ cm`

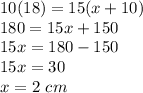
therefore

There is only one value of x that makes BAE and CAD triangles similar