Question

Complete the table of values


`y = {x}^(2) - 2x - 3`
For -2,-1,0,1,2,3,4
​I need help please

Answer 1

Explanation:

Given

`y=x^2-2x-3`

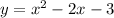
Putting x = -2 in the function

`y=x^2-2x-3`

`y=\left(-2\right)^2-2\left(-2\right)-3`

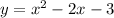
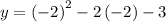
= 4 + 4 - 3

= 5

(x, y) = (-2, 5)

Putting x = -1 in the function

`y=x^2-2x-3`

`y=\left(-1\right)^2-2\left(-1\right)-3`

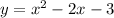
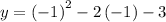
= 1 + 2 - 3

= 0

(x, y) = (-1, 0)

Putting x = 0 in the function

`y=\left(0\right)^2-2\left(0\right)-3`

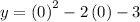
= 0 - 0 -3

= -3

(x, y) = (0, -3)

Putting x = 1 in the function

`y=\left(1\right)^2-2\left(1\right)-3`

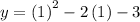
= 1 - 2 - 3

= -4

(x, y) = (1, -4)

Putting x = 2 in the function

`y=\left(2\right)^2-2\left(2\right)-3`

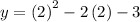
= 4 - 4 - 3

= -3

(x, y) = (2, -3)

Putting x = 3 in the function

`y=\left(3\right)^2-2\left(3\right)-3`

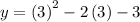
= 9 - 6 - 3

= 0

(x, y) = (3, 0)

Putting x = 4 in the function

`y=\left(4\right)^2-2\left(4\right)-3`

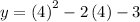
= 16 - 8 - 3

= 5

(x, y) = (4, 5)

Therefore, completing the table:

x y

-2 5

-1 0

0 -3

2 -4

3 0

4 5