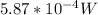Answer:
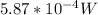
Step-by-step explanation:
Given that:
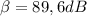

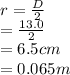
Efficiency = 2.06 % = 0.0206
The intensity level of sound is given by the formula:
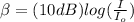
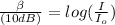
Taking their exponential; we have :
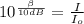
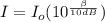
Replacing our values; we have:
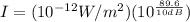
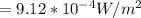
Power Output;
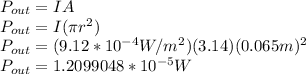
The power output that is required to produce a 89.6 dB sound intensity level for a 13.0 cm diameter speaker that has an efficiency of 2.06% is;
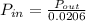
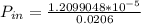
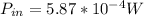
Therefore, The power output that is required to produce a 89.6 dB sound intensity level for a 13.0 cm diameter speaker that has an efficiency of 2.06% is