Question

(a) Show that every member of the family of functions y = (6 ln(x) + C)/x , x > 0, is a solution of the differential equation x2y' + xy = 6. (Simplify as much as possible.)

Answer 1

Therefore , every element of the function
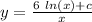`y =(6 \ ln (x)+c)/(x)` is a solution of the DE
`x^2y'+xy=6`.

Explanation:

Given differential equation is

`x^2y'+xy=6`

`\Rightarrow y'+(xy)/(x^2)=(6)/(x^2)` [ divided by x²]

`\Rightarrow y'+(y)/(x)=(6)/(x^2)`

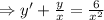
Here
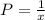`P= (1)/(x)` and
`Q=(6)/(x^2)`

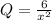
The integrating factor is =
`e^(\int pdx)`

`=e^{\int (1)/(x)dx`

`=e^(ln x)`

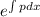
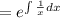
= x

Multiplying the integrating factor both sides of the ODE

`x y'+x.(y)/(x)=x. (6)/(x^2)`

`\Rightarrow xy'+y=(6)/(x)`

`\Rightarrow x(dy)/(dx)+y=(6)/(x)` [
`\because y'=(dy)/(dx)` ]

`\Rightarrow xdy+ydx=(6)/(x)dx`

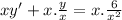
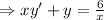
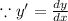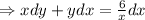
Integrating both sides

`\int xdy+\int ydx=\int(6)/(x)dx`

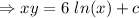`\Rightarrow xy= 6\ ln(x)+c` [ c is an arbitrary constant]

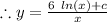`\therefore y =(6 \ ln (x)+c)/(x)` for x>0

Therefore , every element of the function
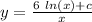`y =(6 \ ln (x)+c)/(x)` is a solution of the DE
`x^2y'+xy=6`.