Answer:
So the points of tangency are:
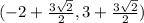
and
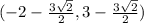
Explanation:

Since the instructions are to find the points of tangency where the slopes are -1, we will need ti find the derivative.
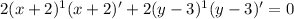
I used chain rule on the left and constant rule on the right.
Let's finish differentiating the insides:
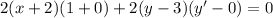
Simplify:
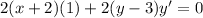
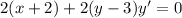
Now we want to isolate
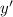 .
.
Subtract
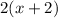 on both sides:
on both sides:
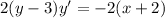
Divide both sides by
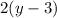 :
:
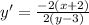
Simplify:
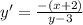
We want to find the points such that:
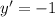

Multiply both sides by
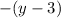 :
:
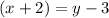
Add
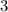 on both sides:
on both sides:
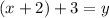
Distribute:
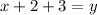
Simplify:
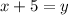
So we want to find the points such that the following two equations are satisfied:


Let's replace
 with
with
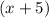 :
:
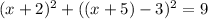
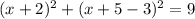

Combine like terms:
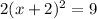
Divide both sides by 2:
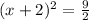
Take square root of both sides:
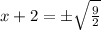
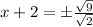
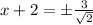
Rationalize denominator by multiplying top and bottom by
 for right hand side:
for right hand side:

Subtract 2 on both sides:
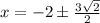
Now let's find the corresponding
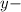 coordinates.
coordinates.

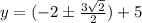
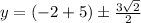
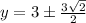
So the points of tangency are:
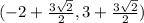
and
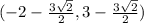
---------------------Adding geometric/algebra approach here------
 has center (-2,3) and radius 3.
has center (-2,3) and radius 3.
I put a drawing to show sort of what we are looking for.
We can find the point of tangency by finding where the green line is perpendicular to while going through center of circle which is (-2,3).
Perpendicular lines have opposite reciprocal slopes. The opposite reciprocal of -1 is 1/1 =1 (so just 1 is the slope of the line perpendicular to the green line. The purple line that I drew will represent our perpendicular line.
So we are looking for a line with slope 1 and goes through point (-2,3).
Slope-intercept form is
 .
.
We know
 :
:
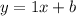
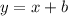
We can find
 using (-2,3):
using (-2,3):
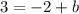
Add 2 on both sides:

So the line is
 which is the line we found during our calculus approach.
which is the line we found during our calculus approach.