Question

One year Roger had the lowest ERA​ (earned-run average, mean number of runs yielded per nine innings​ pitched) of any male pitcher at his​ school, with an ERA of 3.14. ​Also, Amber had the lowest ERA of any female pitcher at the school with an ERA of 3.38. For the​ males, the mean ERA was 4.371 and the standard deviation was 0.787. For the​ females, the mean ERA was 4.363 and the standard deviation was 0.869. Find their respective​ z-scores. Which player had the better year relative to their​ peers, Roger or Amber​? ​(Note: In​ general, the lower the​ ERA, the better the​ pitcher.) Roger had an ERA with a​ z-score of nothing. Amber had an ERA with a​ z-score of nothing.

Answer 1

(a) The z-score of Roger is -1.56 and the z-score of Amber is -1.13.

(b) Roger had a better year relative to his peers.

Explanation:

If X follows N (µ, σ₂), then
`z=(x-\mu)/(\sigma)`, is a standard normal variate with mean, E (Z) = 0 and Var (Z) = 1. That is, Z follows N (0, 1).

Let X = ERA of male pitchers and Y = ERA of ERA of female pitchers.

It is provided that the mean and standard deviation of X are:

`\mu_(X)=4.371\\\sigma_(X)=0.787`

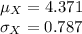
Also, the mean and standard deviation of Y are:

`\mu_(Y)=4.363\\\sigma_(Y)=0.869`

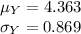
ER of Roger is 3.14 and ERA of Amber is 3.38.

(1)

Compute the z-score of Roger as follows:

`z=(x-\mu_(X))/(\sigma_(X))=(3.14-4.371)/(0.787)=-1.56`

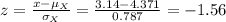
Thus, the z-score of Roger is -1.56.

Compute the z-score of Amber as follows:

`z=(x-\mu_(Y))/(\sigma_(Y))=(3.38-4.363)/(0.869)=-1.13`

Thus, the z-score of Amber is -1.13.

(2)

Compute the probability of ERA's that are greater than Roger's ERA as follows:

`P(X>3.14)=P((X-\mu)/(\sigma)>(3.14-4.371)/(0.787))\\=P(Z>-1.56)\\=P(Z<1.56)=0.9406`

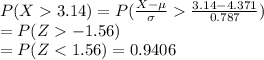
This implies that 94% of the other male pitchers had an ERA higher than 3.14.

Compute the probability of ERA's that are greater than Amber's ERA as follows:

`P(Y>3.38)=P((Y-\mu_(Y))/(\sigma_(Y))>(3.38-4.363)/(0.869))\\=P(Z>-1.13)\\=P(Z<1.13)=0.8708`

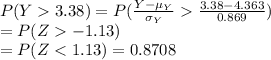
This implies that 87% of the other female pitchers had an ERA higher than 3.38.

As it is provided that the lower the ERA the better the pitcher, then it can be concluded that Roger had a better year relative to his peers.