Question

In a study of the progeny of rabbits, Fibonacci (ca. 1170-ca. 1240) encountered the sequence now bearing his name. The sequence is defined recursively as follows.

an + 2 = an + an + 1, where a1 = 1 and a2 = 1.

(a) Write the first 12 terms of the sequence.

Answer 1

The correct answer is 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.

Explanation:

In a study of the progeny of rabbits, Fibonacci encountered the sequence now bearing his name.

The sequence is defined recursively as:

`a_(n+2)` =
`a_(n)` +
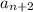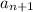`a_(n+1)`, where a1 = 1 and a2 = 1 where n is a natural number.

For n = 0 ; a2 = a0 + a1

⇒ a0 = 0.

For n = 1 ; a3 = a1 + a2 = 1+1

⇒ a3 = 2.

For n = 2 ; a4 = a2 + a3 = 1+2

⇒ a4 = 3.

For n = 3 ; a5 = a3 + a4 = 2+3

⇒ a3 = 5.

For n = 4 ; a6 = a4 + a5 = 3+5

⇒ a6 = 8.

For n = 5 ; a7 = a5 + a6 = 5+8

⇒ a7 = 13.

For n = 6 ; a8 = a6 + a7 = 8+13

⇒ a8 = 21.

For n = 7 ; a9 = a7 + a8 = 21+13

⇒ a9 = 34.

For n = 8 ; a10 = a8 + a9 = 21+34

⇒ a10 = 55.

For n = 9 ; a11 = a9 + a10 = 55+34

⇒ a11 = 89.

Thus the first 12 terms of fibonacci sequence is 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.