Question

A cube of solid benzene (C6H6) at its melting point and weighing 10.0 g is placed in 10.0 g of water at 30 °C. Given that the heat of fusion of benzene is 9.92 kJ/mol, to what temperature will the water have cooled by the time all of the benzene has melted?

Answer 1

Answer: The temperature at which the water has cooled is -0.333°C

Step-by-step explanation:

To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

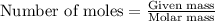
Given mass of benzene = 10 g

Molar mass of benzene = 78 g/mol

Putting values in above equation, we get:

`\text{Moles of benzene}=(10g)/(78g/mol)=0.128mol`

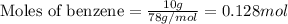
To calculate the heat absorbed, we use the equation:

`\Delta H_(fusion)=(q)/(n)`

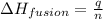
where,

q = amount of heat absorbed = ?

n = number of moles of benzene = 0.128 mole

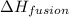`\Delta H_(fusion)` = heat of fusion of benzene = 9.92 kJ/mol = 9920 J/mol (Conversion factor: 1 kJ = 1000 J)

Putting values in above equation, we get:

`9920J/mol=(q)/(0.128mol)\\\\q=(9920J/mol* 0.128mol)=1269.76J`

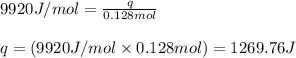
Heat absorbed by benzene will be equal to heat released by water

Sign convention of heat:

When heat is absorbed, the sign of heat is taken to be positive and when heat is released, the sign of heat is taken to be negative.

To calculate the final temperature, we use the equation:

`q=mc\Delta T=mc(T_2-T_1)`

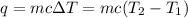
where,

q = heat released by water = -1269.76 J

m = mass of water = 10.0 g

c = heat capacity of water = 4.186 J/g°C

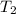`T_2` = final temperature = ?

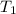`T_1` = initial temperature = 30°C

Putting values in above equation, we get:

`-1269.76J=10g* 4.186J/g^oC* (T_2-30)\\\\T_2=-0.333^oC`

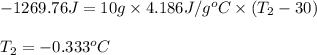
Hence, the temperature at which the water has cooled is -0.333°C