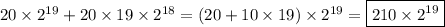I bet the sum you're referring to is supposed to be
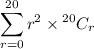
or equivalently,
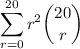
where
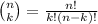 is the binomial coefficient.
is the binomial coefficient.
Recall the binomial series,
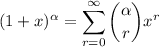
which is valid for |x| < 1. (Note that if r > α, the binomial coefficient is defined to be zero, so there really are only α many terms when α is a whole number.)
Differentiating both sides with respect to x gives
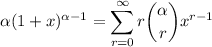
Multiply both sides by some arbitrary x in |x| < 1 :
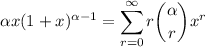
Repeat:
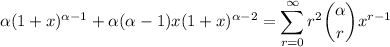
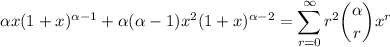
Let α = 20, and let x approach 1 from below. The right side converges to the sum we want, while the left side converges to