Question

A process that produces computer chips has a mean of .04 defective chip and a standard deviation of .003 chip. The allowable variation is from .03 to .05 defective. a. Compute the capability index for the process. b. Is the process capable?

Answer 1

A. 1.111

B. The process is not capable

Step-by-step explanation:

Part A

Capacity index help to determine the performance of a process and how it could perform in the future. A capacity index of above 1.33 means that the process is capable but a capacity index below 1.33 means that the process is not capable. The capacity index can be calculated using equation 1;

From the mean which is 0.5, it can be determined that the process is a centered process.

For centered process, the mean = 0.5 x (Upper s. - Lower S.) = 0.5 x 0,02 = 0.04

so the capacity index for centered mean will be used

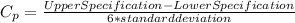`C_(p) =(Upper Specification-Lower Specification)/(6 * standard deviation)` ................................................1

Given standard deviation = 0.003

upper specification = 0.05

lower specification = 0.03

`C_(p) =(0.05- 0.03)/(6 * 0.003)\\\\C_(p) = (0.02)/(0.018) \\\\C_(p) = 1.111`

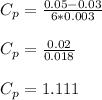
Therefore the capacity index of the process is 1.111

Part B

The capacity index of the process is 1.111 and it is less than 1.33, this means that the process is not capable.