Answer:
Explanation:
The displacement function is given by
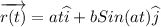 .... (1)
.... (1)
Differentiate both sides with respect to t on both the sides
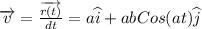
Differentiate again with respect to t to get the function of acceleration
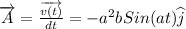
where, A is the acceleration
So, by equation (1)
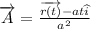
So, the acceleration is proportional to the displacement function.