Question

Question: If
`$f(x)=\cos \left[2 \tan ^(-1)\left(\sin \left(\cot ^(-1) \sqrt{(1-x)/(x)}\right)\right)\right]$`

Options:

`(a) $f^(\prime)(x)(x-1)^(2)-2(f(x))^(2)=0$\\\(b) $f^(\prime)(x)(x-1)^(2)+2(f(x))^(2)=0$\\(c) $f^(\prime)(x)(x+1)^(2)+2(f(x))^(2)=0$\\(d) $f^(\prime)(x)(x+1)^(2)-2(f(x))^(2)=0$`

Answer 1

Note that √((1 - x)/x) is defined only as long as 0 < x ≤ 1.

Consider a right triangle with reference angle θ such that

`\cot(\theta) = \sqrt{\frac{1-x}x}`

In other words, on an appropriate domain,

`\theta = \cot^(-1)\left(\sqrt{\frac{1-x}x}\right)`

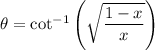
In such a triangle, you would find that

`\sin(\theta) = \sqrt x`

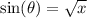
so f(x) reduces a bit to

`f(x) = \cos\left(2 \tan^(-1)(\sqrt x)\right)`

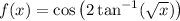
Now consider another triangle with reference angle ɸ such that

`\tan(\phi) = \sqrt x \implies \phi = \tan^(-1)(\sqrt x)`

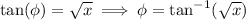
In this triangle, you would find

`\cos(\phi) = \frac1{√(1+x)}`

Recalling the double angle identity for cosine, it follows that

`f(x) = \cos(2\phi) = 2 \cos^2(\phi) - 1 = (1-x)/(1+x)`

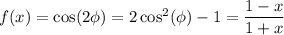
Differentiating with respect to x yields

`f'(x) = -\frac2{(1+x)^2}`

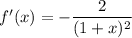
while

`f(x)^2 = ((1-x)^2)/((1+x)^2)`

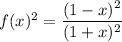
It follows that

`f'(x)(x-1)^2 - 2f(x)^2 = 0`

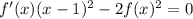
so B is the correct choice.