Answer:
160 Hz.
Step-by-step explanation:
For nth harmonic, the fundamental frequency,

Here T is the tension in string, \mu is the mass/unit of length of the string and L is the string length.
Given n = 1 frequency of the 1st harmonic (the Fundamental), T = 859 N,
L= 339 cm =3.39 m and
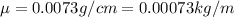 .
.
Substituting these values, we get
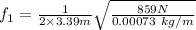


Thus, the fundamental frequency is 160 Hz.